Mouvement Brownien & théorie du potentiel
Le théorème de Kakutani (1944) établit un lien entre la théorie classique du potentiel et le mouvement Brownien. On en propose ci-dessous une approche "expérimentale" bidimensionnelle, en utilisant pour simplifier des marches aléatoires isotropes sur un résean plan.
- Mouvement Brownien & théorie du potentiel ... (à paraitre)
- Fichier Mathematica

Problème de Dirichlet sur un domaine Ω rectangulaire
Soit Ω le rectangle de coté a et b (sur la figure, on a pris a = 2b). On cherche un potentiel électrostatique V(x,y) harmonique sur Ω vérifiant les conditions aux limites de Dirichlet suivantes :
- V(x,y) = 0 sur les conducteurs "horizontaux" ;
- V(x,y) = V1 sur le conducteur "vertical" x = 0 ;
- V(x,y) = V2 sur le conducteur "vertical" x = a.
La solution exacte est de la forme :
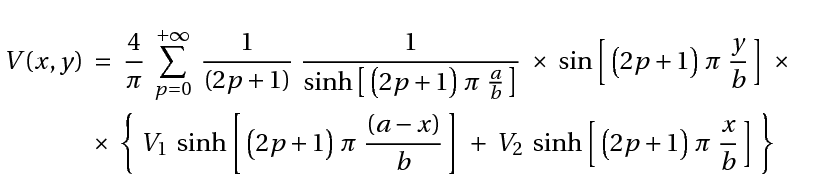
La figure ci-dessus, qui montre les lignes de champs électrique (flèches) et les équipotentielles (pointillés), a été tracée pour V1 = + 6 V, et V2 = + 2 V.
© 2012
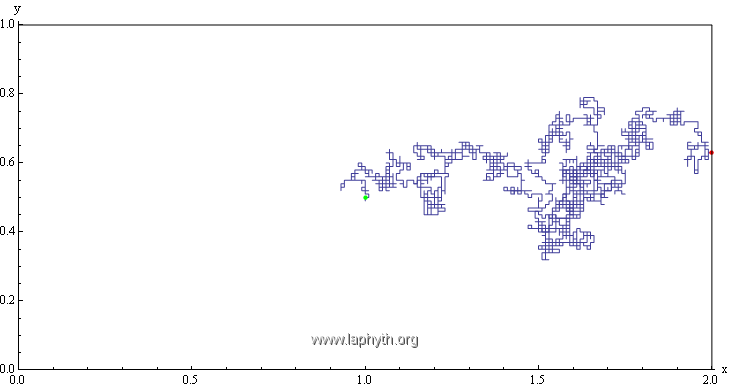
Solution Brownienne du problème de Dirichlet
Pour calculer la valeur du potentiel électrostatique V(x,y) au point vert, on démarre un mouvement Brownien (ici, une marche aléatoire) en ce point. On stoppe ce mouvement Brownien lorsqu'il atteint la frontière du domaine pour la première fois (ici, au point rouge). Le théorème de Kakutani affirme que le potentiel au point vert est égal à la moyenne statistique Brownienne des potentiels aux points rouges ...
© 2012