Marche aléatoire sur la sphère
- Enoncé (à paraitre)
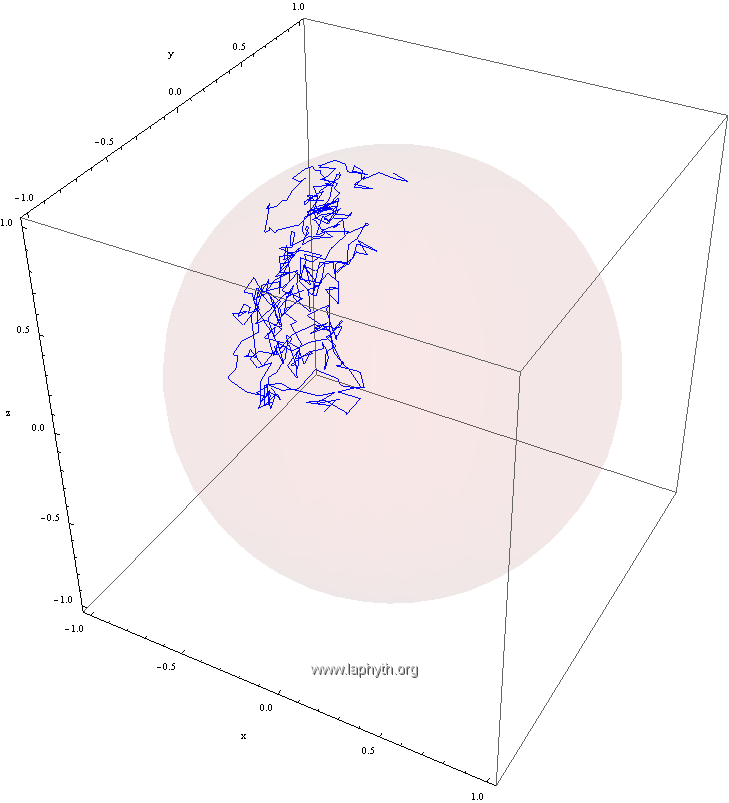
Réalisation d'une marche aléatoire géodésique isotrope sur la sphère.
Cette marche aléatoire de 500 pas sur la sphère de rayon unité est issue du pôle Nord.
© 2012
Si un lien ne fonctionne plus, merci de le signaler

Réalisation d'une marche aléatoire géodésique isotrope sur la sphère.
Cette marche aléatoire de 500 pas sur la sphère de rayon unité est issue du pôle Nord.
© 2012
Le "disque de Poincaré" est un modèle de géométrie hyperbolique (géométrie non-euclidienne à courbure négative constante). On peut le voir comme le disque de rayon unité, sur lequel un point est repéré par ses coordonnées polaires usuelles, mais où la métrique (carré de la distance élémentaire entre ce point et un point voisin) est donnée par :

La présence du dénominateur introduit une "distorsion" des distances par rapport à la métrique euclidienne usuelle (*). En particulier, le bord du disque de Poincaré (r=1) est situé à une distance hyperbolique infinie de tout point à l'intérieur du disque.
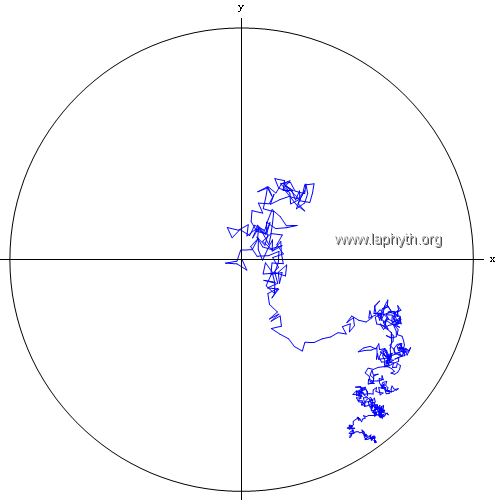
Réalisation d'une marche aléatoire géodésique isotrope sur le disque de Poincaré.
Cette marche aléatoire de 800 pas est issue du centre du disque. Tous les pas ont ici la même longueur hyperbolique. En raison de la distorsion introduite par le dénominateur de la métrique, ils nous semblent d'autant plus petits que l'on s'éloigne du centre, mais ceci n'est qu'une illusion d'optique "euclidienne".
© 2012
(*) Cette distorsion de longueurs fût une source d'inspiration pour le graveur néerlandais M.C. Escher (1898-1972), avec notamment la célèbre série des "Circle Limit", dont un représentant figure ci-dessous :

M.C. Escher ; Circle Limit IV (1960)