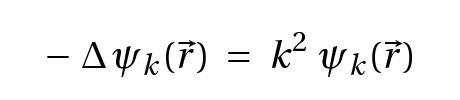
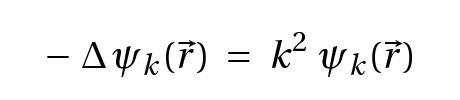
L'origine physique du problème mathématique remonte à la seconde moitié du XIXe siècle, avec l'observation expérimentale de l'universalité des propriétés du rayonnement thermique d'équilibre contenu dans une cavité dont les parois sont maintenues à une température constante ("rayonnement du corps noir"). En particulier, la densité volumique spectrale d'énergie du rayonnement d'équilibre est indépendante de la géométrie exacte de la cavité.
En 1859, Kirchhoff reliera cette universalité au second principe de la thermodynamique. Ce caractère universel amènera Planck à s'intéresser au problème du rayonnement du corps noir. C'est pour reproduire la courbe expérimentale de cette densité volumique spectrale d'énergie que Planck introduira l' « hypothèse des quanta » en 1900.
Pour simplifier, ces propriétés sont illustrées ci-dessous sur des exemples bidimensionnels.
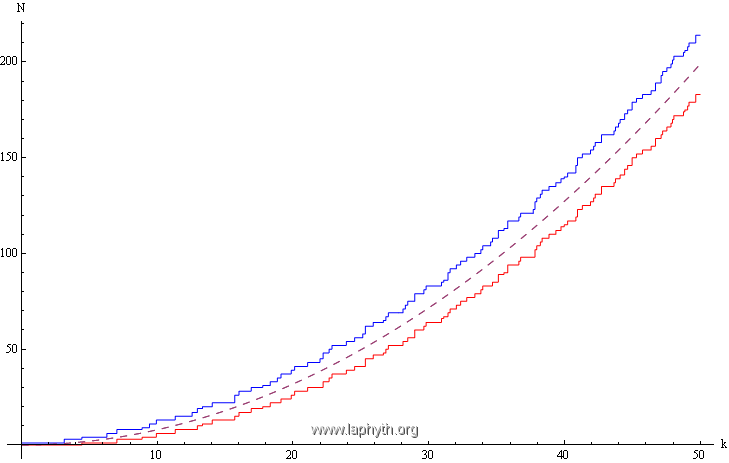
Escalier spectral d'un domaine plan carré de coté unité.
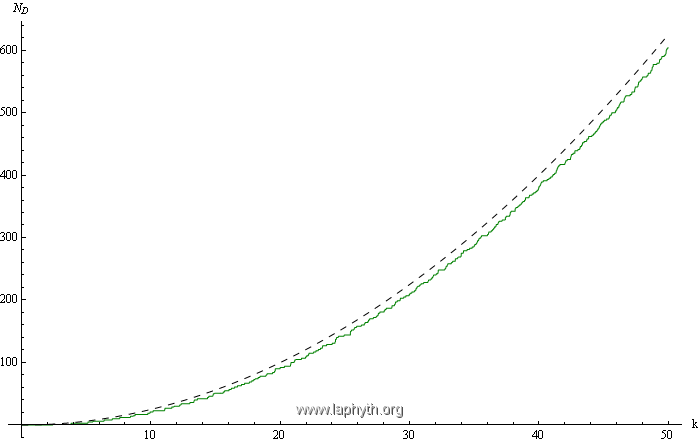
Escalier spectral d'un disque plan de rayon unité avec conditions aux limites de Dirichlet (en vert).
On observe sur les figures précédentes un écart entre l'escalier spectral exact (qui dépend des conditions aux limites) et l'asymptotique de Weyl, universelle. Cet écart est quantifié ci-dessous : au terme de surface s'ajoute une correction de périmètre (*).
(*) En dimension trois, au terme de volume s'ajouterait une correction de surface.
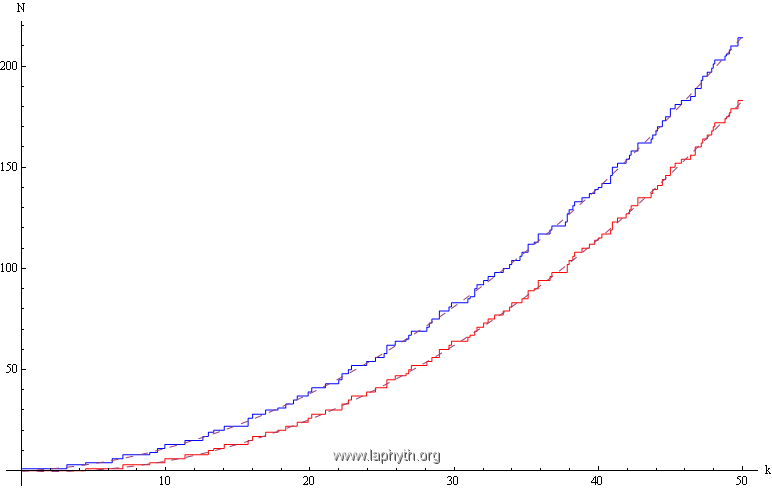
Escalier spectral d'un domaine plan carré de coté unité (rouge = CL Dirichlet, bleu = CL Neumann).
L'asymptotique de Weyl est ici corrigée par un terme sous-dominant qui dépend des conditions aux limites (courbes en pointillés) :

Le signe moins correspond aux conditions aux limites de Dirichlet, le signe plus correspond aux conditions aux limites de Neumann.
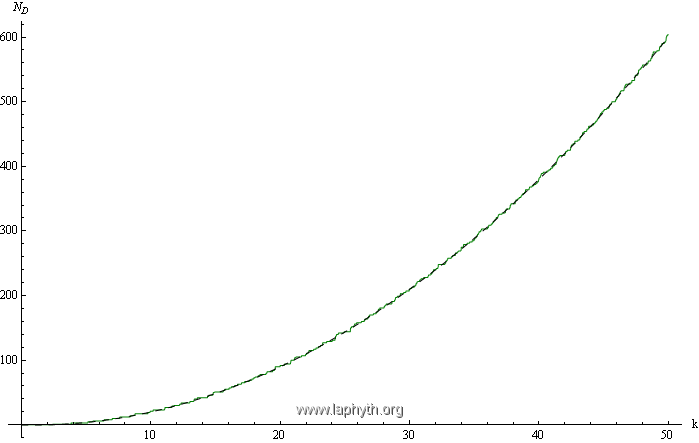
Asymptotique de Weyl (avec correction de frontière) pour un disque plan de rayon unité muni de conditions aux limites de Dirichlet.
© 2012