Formule de Stokes

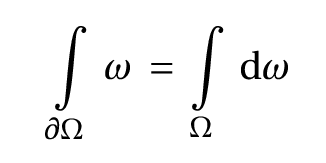
Mathématicienne et membre de l’Oulipo ¹,  Michèle Audin publie : La formule de Stokes, roman, Cassini (2016), ISBN 978-84225-206-9, présentation de l’éditeur.

• Michèle Audin, De la beauté : la formule de Stokes, Images des Mathématiques (2009), web.
• Formulaire d’analyse vectorielle, pdf.
• TD « Méthodes mathématiques pour la théorie des champs » : le langage des formes différentielles, pdf.
• Cours : La formule de Stokes, (en préparation), pdf.

Aspects historiques

• J.J. Cross, Integral theorems in Cambridge mathematical physics, dans : Peter Harman (éditeur), Wranglers and Physicists: Studies on Cambridge Physics in the Nineteenth Century, Manchester University Press (1986), ISBN 978-0719017568.
• Victor J. Katz, The History of Stokes’ Theorem, Mathematics Magazine 52 (3) (May 1979), 146-156, doi.org/10.1080/0025570X.1979.11976770
• Charles H. Stolze, A history of the divergence theorem, Historia Mathematica 5 (4) (November 1978), 437-442, doi:10.1016/0315-0860(78)90212-4.
• Victor J. Katz, The history of differential forms from Clairaut to Poincaré, Historia Mathematica 8 (2) (May 1981), 161-188, doi:10.1016/0315-0860(81)90027-6.

• Mark McCartney, Andrew Whitaker et Alastair Wood (éditeurs), George Gabriel Stokes — Life, Science and Faith, Oxford University Press (2019), ISBN 978-0-1988-2286-8, présentation de l’éditeur.

Panorama mathématique récent

• Silvana S. S. Cardoso, Julyan H. E. Cartwright, Herbert E. Huppert et Christopher Ness (éditeurs), Stokes at 200: a celebration of the remarkable achievements of Sir George Gabriel Stokes two hundred years after his birth, Philosophical Transactions of the Royal Society (2020), 2 parties :
• part 1: Volume 378, Issue 2174, doi.org/10.1098/rsta.2019.0505
• part 2: Volume 378, Issue 2179, doi.org/10.1098/rsta.2020.0160

• Sir Michael Atiyah, Sir G.G. Stokes’s influence on differential geometry, The Isaac Newton Institute for Mathematical Sciences (2003) : vidéo indisponible.

Notes