Il y a un peu plus de cinquante ans que George Uhlenbeck et moi [Samuel Goudsmit] avons introduit le concept de « spin ». Les Etats-Unis, qui fêtent leur bicentenaire, sont seulement quatre fois plus vieux que le spin — même pas un ordre de grandeur de plus ! Il n’est donc pas surprenant que la plupart des jeunes physiciens ne sachent pas que le spin devait être introduit. Ils pensent qu’il a été révélé dans la Genèse, ou peut-être postulé par Sir Isaac Newton, deux évènements que les jeunes considèrent comme à peu près simultanés. [...]
En comparaison de l’impitoyable compétition pour la reconnaissance que subissent les physiciens contemporains hautement spécialisés, l’atmosphère du « printemps de la physique atomique moderne » ressemblait à celle d’un « Peyton Place 1 sans sexe ».2
Documents
- Effet Zeeman : vidéo 1 + vidéo 2
- Expérience de Stern et Gerlach : vidéo + ADS + TD.
- TD « Moment cinétique, spin, and all that … », pdf.
- TD « Modèle classique du spin ? », pdf.
Spin et magnétisme
Em mécanique quantique, le spin est un opérateur vectoriel dont les composantes possèdent les mêmes relation de commutation que celles du « moment cinétique » :
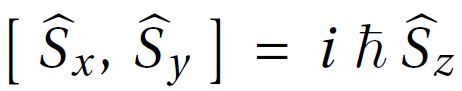
C’est en ce sens (abstrait) que :
« Le spin est une caractéristique quantique des particules intimement liée à leurs propriétés de rotation. » 3
b.a.ba.
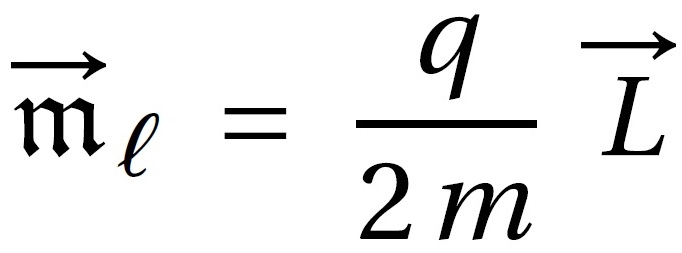
Le moment magnétique orbital est proportionnel au moment cinétique. La constante de proportionnalité q/2m est le « rapport gyromagnétique ».
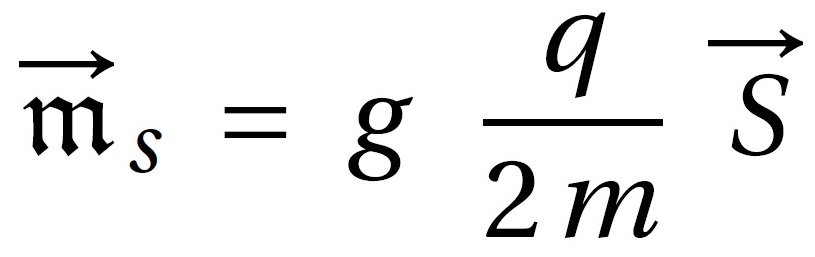
Le moment magnétique de spin est proportionnel au spin. La constante g sans dimension est le « facteur de Landé » de la particule.
Anomalie
Pour l’électron (de spin 1/2), la théorie quantique et relativiste de Dirac (1928) prédit la valeur exacte : g = 2. Jusqu’en 1947, les expériences semblaient confirmer cette valeur.
En 1947, Kusch et Fowley réalisent une expérience de résonance magnétique sur des atomes de gallium, indium et sodium ; ces expérimentateurs mettent en évidence l’existence d’une « anomalie » – écart normalisé à la valeur de Dirac — non-nulle : a ≠ 0

L’expérience de Kusch et Fowley est discutée à la conférence de Shelter Island à laquelle assistent notamment Feynman et Schwinger. En 1948, Schwinger réussit le premier calcul de l’anomalie de l’électron à l’aide de l’électrodynamique quantique au second ordre de la théorie de perturbation 4 :

α est la « constante de structure fine » de Sommerfeld (1916).

Tombe de Schwinger (cimetière de Mount Auburn -- Cambridge - Massachusetts)
Moment magnétique anormal du muon
Cousin lourd de l’électron, le muon appartient à la famille des leptons, particules élémentaires insensibles à l’interaction nucléaire forte. Ces particules sont des fermions de spin 1/2, auquel est associé un « moment magnétique de spin ».
Les analyses les plus récentes montrent qu’il n’existe pas de tension entre la prédiction théorique du Modèle Standard de la physique des particules et les derniers résultats expérimentaux.
Orientation bibliographique
- Jean-Marc Lévy-Leblond, Qu’est-ce que le spin ?, Pour la Science 473 (février 2017), web
- Hans C. Ohanian, What is spin?, American Journal of Physics 54 (1986), 500-505, doi.org/10.1119/1.14580
- Séminaire Poincaré, Le spin, (2007), pdf
- Etienne Klein et Jacques Ball, Et si, pour une fois, on osait parler du spin ?, France-Culture (2016), web. 5
- Jean-Marc Le Goff et Fabienne Kunne, Proton : COMPASS à la recherche du spin manquant, Reflets de la Physique 23 (mars 2011), 14-18, pdf.
Aspects historiques
 Sin-Itiro Tomonaga, The Story of Spin, The University of Chicago Press (1997), ISBN 0-226-80794-0, présentation de l’éditeur.
Sin-Itiro Tomonaga, The Story of Spin, The University of Chicago Press (1997), ISBN 0-226-80794-0, présentation de l’éditeur.- Abraham Pais, George Uhlenbeck & the Discovery of the Electron Spin, Physics Today 42 (12) (décembre 1989), 34-40, pdf.
- Samuel A. Goudsmit, La découverte du spin de l’électron, Journal de Physique 28 (1) (1967), 123-128, pdf.
- Samuel A. Goudsmit, Fifty years of spin: it might as well be spin, Physics Today 29 (6) (1976), 40.
- Samuel A. Goudsmit, The Discovery of the Electron Spin, Université de Leyde, web.
- Horst Schmidt-Böcking, Lothar Schmidt, Hans Jürgen Lüdde, Wolfgang Trageser et Tilman Sauer, The Stern-Gerlach Experiment Revisited, The European Physical Journal H 42 (2016), 1–38, doi: 10.1140/epjh/e2016-70053-2 et arXiv:1609.09311 [physics.hist-ph].
Moment magnétique anormal
- Fermilab, Final Muon g-2 Measurement at Fermilab, vidéo
- Michael Schirber, Muon Experiment Calls It a Wrap, Physics 18 (10 juin 2025), 116, web
- Michel Davier, Zhiqing Zhang, Laurent Lellouch et Bogdan Malaescu, Do muons wobble faster than expected?, CERN Courrier 65 (2) (26 March 2025), 21-25, pdf
- R. Aliberti et al., The anomalous magnetic moment of the muon in the Standard Model: an update, Report number: CERN-TH-2025-101, FERMILAB-PUB-25-0344-T, INT-PUB-25-015, IPARCOS-UCM-25-029, KEK Preprint 2025-22, LTH 1403, MITP-25-037, UWThPh 2025-15, ZU-TH 37/25, (27 mai 2025), doi.org/10.48550/arXiv.2505.21476
Aspects historiques
- B. Lee Roberts et William J Marciano (éditeurs), Lepton Dipole Moments, Advanced Series on Directions in High Energy Physics 20 (2009), World Scientific (2009), doi.org/10.1142/7273
- Silvan S. Schweber, QED and the Men Who Made It : Dyson, Feynman, Schwinger and Tomonaga, Princeton University Press (1994), ISBN 978-0-691-03327-3.

QED et le moment magnétique anormal de l'électron : de l'expérience de Kusch et Fowley (1947) au calcul de Schwinger au second ordre de la théorie de perturbation (1948).
- Jagdish Mehra, The Beat of a Different Drum: The life and science of Richard Feynman, Oxford University Press (1994), ISBN 0-19-853948-7.
- Jagdish Mehra et Kimball A. Milton, Climbing the Mountain: The Scientific Biography of Julian Schwinger, Oxford University Press (2000), ISBN 978-0-19-850658-4
- Robert P. Crease et Makiko Nio, Toichiro Kinoshita – Biographical Memoir, National Academy of Science (2023), pdf

Kinoshita et Feynman en 1961
Notes
- Peyton Place : soap opera américain diffusé par la chaine de télévision ABC entre 1964 et 1969. ↩
- Samuel A. Goudsmit, Fifty years of spin: it might as well be spin, (1976), cf. supra. ↩
- J. M. Lévy-Leblond (cf. bibliographie). ↩
- Ce calcul de Schwinger est un véritable tour de force : la dérivation repose sur une astucieuse succession de transformations canoniques dont l’esprit est résumé dans le livre de Schweber (cf. bibliographie). En 1948, la méthode diagrammatique de Feynman était encore dans les limbes ; cf. le fiasco de ce dernier à la conférence de Pocono e.g. dans : Silvan S. Schweber, Feynman and the visualization of space-time processes, Reviews of Modern Physics 58 (1986), 449-508, doi.org/10.1103/RevModPhys.58.449 ↩
- La QCD sur réseau évoquée dans l’émission d’Étienne Klein est introduite dans l’article consacré à Ken Wilson. ↩

