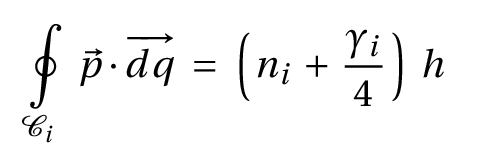« Enrober de chair quantique un squelette classique. » 1
Condition de quantification semi-classique EBK (Einstein-Brillouin-Keller). L'indice de Maslov γ est un invariant topologique associé à la courbe fermée dans l'espace des phases du système intégrable (courbe sur laquelle porte l'intégration).
- TD-Cours : approximation BKW et quantification EBK, pdf.
- TD-Cours : approximation BKW et équation de Hamilton-Jacobi, pdf.
Orientation bibliographique
- André Voros, Aspects de la limite (semi)-classique, Journées X-UPS 5 (1987/1988), 37-48, pdf.
- Yves Colin de Verdière, Une introduction à la mécanique semi-classique, L’Enseignement Mathématique 44 (1998), 23-51, dx.doi.org/10.5169/seals-63894
Ouvrages de référence
- Eric J. Heller, The Semiclassical Way to Dynamics and Spectroscopy, Princeton University Press (2018), ISBN 978-0-691-16373-4.
- Mark S. Child, Semiclassical Mechanics with Molecular Applications, Oxford University Press (2e édition-2014), ISBN 978-0-1996-7298-1.
- Martin C. Gutzwiller, Chaos in classical and quantum mechanics, Springer (1990), ISBN 978-1-4612-6970-0.
- Matthias Brack et Rajat K. Bhaduri, Semiclassical Physics, Frontiers in Physics 96, CRC Press (2003), ISBN 978-0-8133-4084-5.
- Lev Landau et Evgueni Lifchitz, Mécanique quantique, Éditions Mir (3e édition-1975), pp. 193-230.
- Albert Messiah, Mécanique quantique (tome 1), Dunod (1969), pp. 194-202.
- Carl M. Bender et Steven A. Orszag, Advanced mathematical methods for scientists and engineers — Asymptotic methods and perturbation theory, Springer (1999), ISBN 978-0-387-98931-0 (cf. le chapitre 10).
Pour aller plus loin
- Michael V. Berry, Singular limits, Physics Today 55 (5) (May 2002), 10-11, pdf.
- Eric J. Heller et Steven Tomsovic, Postmodern Quantum Mechanics, Physics Today 46 (7) (1993), 38-46, pdf.
- A. Douglas Stone, Einstein’s unknown insight and the problem of quantizing chaos, Physics Today 58 (8) (August 2005), 37-43, pdf.
- Ian C. Percival, Semiclassical theory of bound states, Advances in Chemical Physics 36 (1977), 1-61, doi:10.1002/9780470142554.ch1
- Joseph B. Keller, Semiclassical mechanics, SIAM Review 27 (4) (1985), 485-504, doi:10.1137/1027139
- Michael V. Berry et K.E. Mount, Semiclassical approximations in wave mechanics, Reports on Progress in Physics 35 (1972), 315-397, pdf.
- Michael V. Berry, Semiclassical mechanics of regular and irregular motion, dans : Les Houches Lecture Series XXXVI, G Iooss, R H G Helleman et R Stora (éditeurs), North-Holland (1983), 171-271, pdf.
- Michael V. Berry, Some quantum-to-classical asymptotics, dans : Chaos et physique quantique, Les Houches Lecture Series LII (1989), M-J Giannoni, A Voros et J Zinn-Justin (éditeurs), North-Holland (1991), ISBN 0-444-89277-X, pp. 251-304, pdf.
- Lorenzo J. Curtis et David G. Ellis, Use of the Einstein–Brillouin–Keller action quantization, American Journal of Physics 72 (2004), 1521-1523, dx.doi.org/10.1119/1.1768554
- Gregor Tanner et Klaus Richter, Semiclassical theory of helium atom, Scholarpedia 8 (4) (2013), 9818, web.
- Robert Batterman, Quantum Chaos and Semiclassical Mechanics, Proceedings of the Biennial Meeting of the Philosophy of Science Association 1992 (2), (1992), 50-65, doi.org/10.1086/psaprocbienmeetp.1992.2.192824
La formule des traces de Gutzwiller

La "formule des traces" de Gutzwiller relie le spectre d'énergie quantique d'un système physique au spectre des longueurs des orbites périodiques classiques. Valide dans le régime asymptotique où la constante de Planck tend vers zéro, cette formule permet la quantification semi-classique des systèmes dont la dynamique classique est non-intégrable, et pour lesquels la condition de quantification EBK ne s'applique pas. (La formule de Gutzwiller généralise la formule des traces de Selberg, qui est une formule exacte valide pour le flot géodésique des surfaces compactes à courbure négative constante.)
- Martin C. Gutzwiller, The Semi-Classical Quantization of Chaotic Hamiltonian Systems, dans : Chaos and Quantum Physics, Marie-Joya Giannoni, André Voros et Jean Zinn-Justin (éditeurs), Ecole d’été de Physique Théorique des Houches, Session LII, (1989), Elsevier (1991), 201-249,
- Martin C. Gutzwiller, The origins of the trace formula, dans : Classical, Semiclassical and Quantum Dynamics in Atoms, Lecture Notes in Physics 485 (2007), 8-28, doi.org/10.1007/BFb0105967
- Martin C. Gutzwiller, Path Integrals and The Relation Between Classical and Quantum Mechanics, dans : Path Integrals, G.J. Papadopoulos et J.T. Devreese (éditeurs), NATO Advanced Study Institutes 34, Springer (1978), 163-200, doi.org/10.1007/978-1-4684-9140-1_6
- Martin C. Gutzwiller, The Trace Formula between Classical and Quantum Mechanics, dans : Advances in Solid State Physics 41, Bernhard Kramer (éditeur), Springer (2001), 421-432, doi.org/10.1007/3-540-44946-9_34