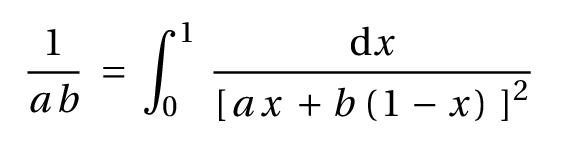Méthodes mathématiques pour la physique théorique

« On vous a sans doute souvent demandé à quoi servent les mathématiques et si ces délicates constructions que nous tirons tout entières de notre esprit ne sont pas artificielles et enfantées par notre caprice.

Parmi les personnes qui font cette question, je dois faire une distinction ; les gens pratiques réclament seulement de nous le moyen de gagner de l’argent. Ceux-là ne méritent pas qu’on leur réponde ; c’est à eux plutôt qu’il conviendrait de demander à quoi bon accumuler tant de richesses et si, pour avoir le temps de les acquérir, il faut négliger l’art et la science qui seuls nous font des âmes capables d’en jouir et propter vitam vivendi perdere causas 1.

D’ailleurs une science uniquement faite en vue des applications est impossible ; les vérités ne sont fécondes que si elles sont enchainées les unes aux autres. Si l’on s’attache seulement à celles dont on attend un résultat immédiat, les anneaux intermédiaires manqueront, et il n’y aura plus de chaine. Les hommes les plus dédaigneux de la théorie y trouvent sans s’en douter un aliment quotidien ; si l’on était privé de cet aliment, le progrès s’arrêterait rapidement et nous nous figerions bientôt dans l’immobilité de la Chine. »  Henri Poincaré (1897) 2

Symétries

  • Henri Bacry, La symétrie ici et là, UTLS (2000) (vidéo)
  • Jean-Bernard Zuber, Symétries en physique, UPMC (2014) (pdf)
« Ce qui gît au plus profond de l’activité théorique, c’est-à-dire au niveau de la construction des modèles, est la recherche des symétries. » Bas C. van Fraassen ; Lois et symétrie (1994)
  • Christophe Eckes, Hermann Weyl – Itinéraire d’un parcours scientifique et intellectuel, Images des Mathématiques, CNRS (2012) (web)
  • David J. Gross, Symmetry in Physics: Wigner’s Legacy, Physics Today (Décembre 1995), 46-50 (pdf)
  • David J. Gross, The role of symmetry in fundamental physics, Proceedings of the National Acadamy of Science (USA) 93 (25) (1996), 14256-14259 (web)
  • Eugene P. Wigner, Events, Laws of Nature, and Invariance Principles, conférence Nobel (1963) (Nobel foundation)
  • Amaury Mouchet, Reflections on the four facets of symmetry: how physics exemplifies rational thinking, European Physical Journal H 38 (2013), 661 (pdf)

David Hilbert, Sur les problèmes futurs des mathématiques (1900)

Analyse harmonique : Fourier & Co.

  • Formulaire (pdf)
  • Animations (Mathematica)
  • Transformée de Fourier discrète ; transformée de Fourier rapide (pdf)
  • Maurice Françon, La transformation de Fourier et ses applications en physique, CERIMES (1966) (vidéo)

Fonctions spéciales de la physique mathématique

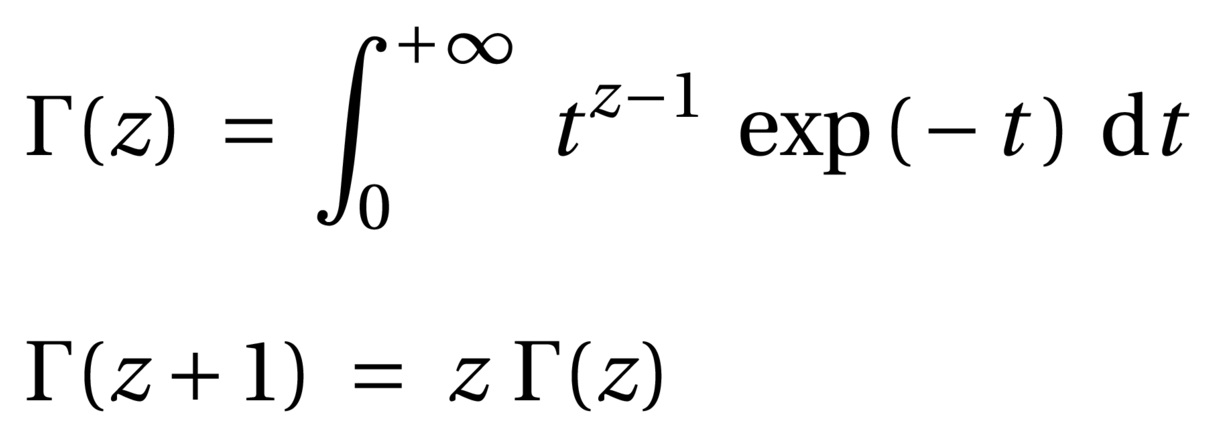
Fonction Gamma d'Euler

  • NIST, Digital Library of Mathematical Functions (web)
  • INRIA, Encyclopedia of Special Functions (web)
  • Abramowitz et Stegun, Handbook of Mathematical Functions (web)
  • Gradshteyn et Ryzhik, Table of Integrals, Series, and Products (web)

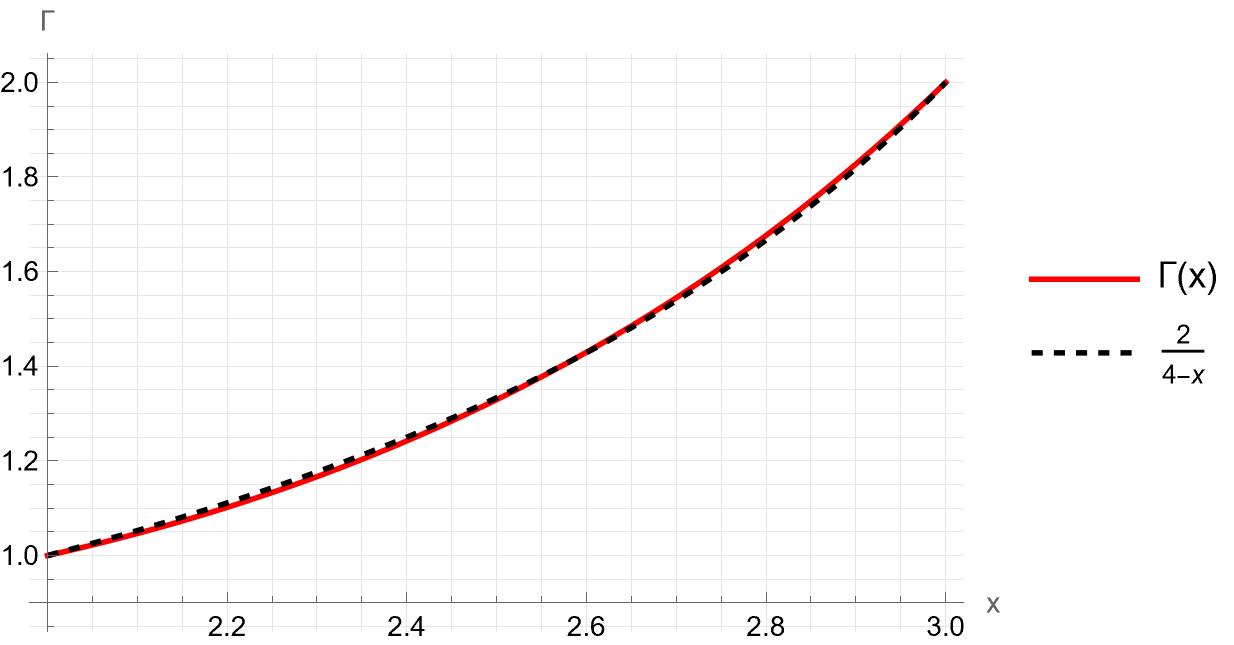
Curiosité : sur cet intervalle, Gamma est bien approximée par une fonction simple.

Équations aux dérivées partielles

  • Théorie du potentiel — Équation de Laplace et équation de Poisson (pdf)
  • Potentiel newtonien : singularité et régularisation (pdf)
  • Équation de Laplace en dimension deux — Invariance conforme (pdf)
  • Théorie du champ vectoriel (pdf)
  • Formulaire d’analyse vectorielle (pdf)
  • Bibliographie

« Les Mathématiques sont une science où l’on ne sait jamais de quoi l’on parle, ni si ce que l’on dit est vrai. » 3

Distribution de Dirac

  • Introduction (pdf)

Théorie des perturbations

« Schrodinger’s papers solved the hydrogen atom. He then proceeded to apply perturbation theory to get the Stark effect. It was my task to present his perturbation theory to the seminar. And I have used perturbation theory ever since, whether it was applicable or not. » 4

« Divergent series converge faster than convergent series because they don’t have to converge. » 5

  • Rudiments et applications (pdf)

« Mathematics should be used in an artistic manner. » 6

Fonctions de Green

  • Introduction (pdf)

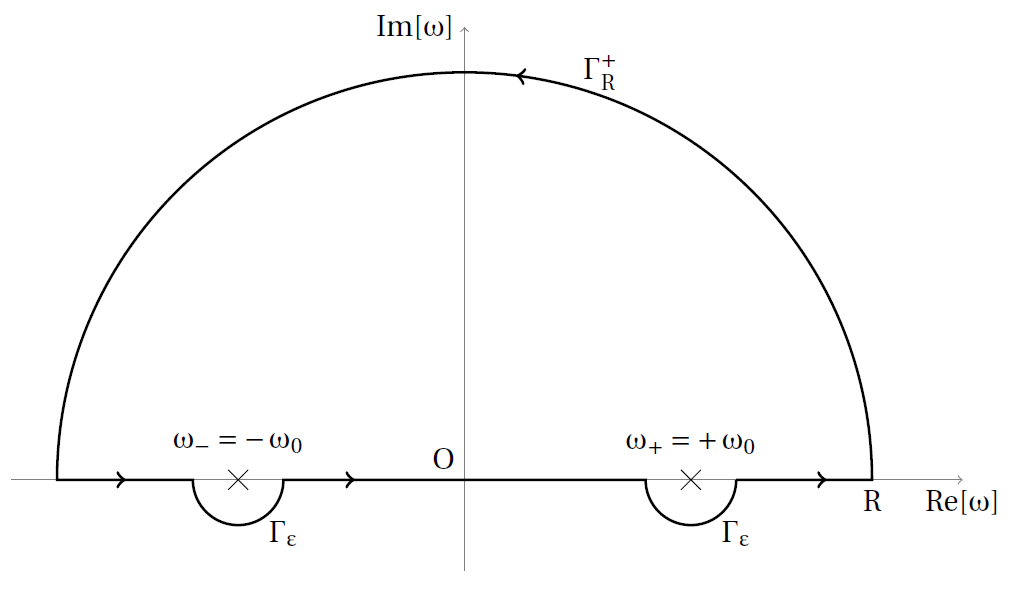
Géométrie différentielle

  • Courbure et torsion d’une courbe gauche (pdf)
  • Courbure d’une surface lisse ; notion de « tenseur de courbure » de Riemann (pdf)
  • Tohru Eguchi, Peter B. Gilkey and Andrew J. Hanson, Gravitation, Gauge Theories and Differential Geometry, Physics Reports 66 (6) (1980), 213-393, (pdf)

 

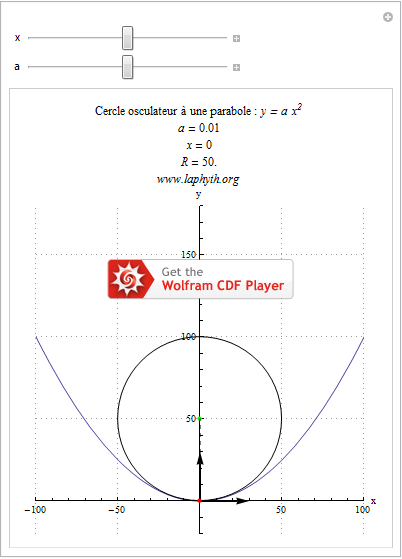
Cercle osculateur à une parabole. En rouge, le point de tangence du cercle et de la parabole. En vert, le centre du cercle. Le rayon de courbure locale R est représenté en tiretés. (Dans un souci de lisibilité, la longueur des vecteurs unitaires de la base locale de Serret-Frenet a été multipliée par 30.)

Calcul des probabilités

  • Probas (I) : distributions discrètes (pdf)
  • Probas (II) : distributions continues (pdf)

Notes

  1. « Pour vivre, perdre la raison de vivre. » Juvénal (poète satirique latin de la fin du siècle I et du début du siècle II.) ↩
  2. Henri Poincaré, Sur les rapports de l’analyse pure et de la physique mathématique, Acta Mathematica 21 (1897), 331-341 ↩
  3. Bertrand Russel, cité par Émile Borel dans : François Le Lionnais (éditeur), Les grands courants de la pensée mathématique, Cahiers du Sud (1948), réédité par Hermann (1998), ISBN 2-7056-6332-0, p. 25 ↩
  4. Hans Bethe (1906-2005), prix Nobel de physique 1967. ↩
  5. George F. Carrier (1918 – 2002). ↩
  6. Hendrik Kramers, cité dans : Max Dresden, H.A. Kramers — Between Tradition and Revolution, Springer (1987), ISBN 0-387-96282-4 (p. 467). ↩

Les commentaires sont fermés.